Треугольник ABC-равнобедренный, АВ=ВС. Через середину стороны АВ провели...

Question

Треугольник ABC-равнобедренный, АВ=ВС. Через середину стороны АВ провели прямую,перпендикулярную к прямой ВС, которая пересекает отрезок ВС в точке D, а прямую АС- в точке К так, что АК=1\2 АВ и ВD=2. Найти периметр треугольника АВС. (желательно с рисунком)

Answer 1

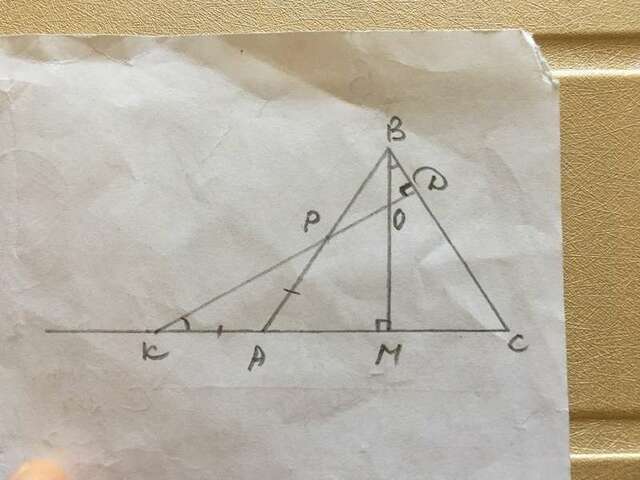
Точка Р - середина стороны АВ. АК=АВ/2 ⇒АК=АР.
Треугольник КАР равнобедренный, АК=АР.
Обозначим ∠РКА=α ⇒ ∠КРА=∠BРД=α.
ВМ - высота тр-ка АВС. ВМ и КД пересекаются в точке О.
Прямоугольные тр-ки КОМ и ВДО подобны, т.к. ∠КОМ=∠ВОД как вертикальные, значит ∠ОВД=∠РКА=α. ВМ - высота и биссектриса равнобедренного тр-ка АВС, значит ∠АВС=2α.
В прямоугольном тр-ке РВД  ∠BРД+∠PBД=α+2α=90°,
3α=90°,
α=30°. Катет ВД лежит напротив в этого угла, значит РВ=2ВД=2·2=4.
АВ=2РВ=2·4=8.
В равнобедренном тр-ке АВС угол при вершине 2α=60°, значит он правильный.
Периметр тр-ка АВС: Р=3АВ=3·8=24 - это ответ.

---