В трапеции ABCD основание ВС равно 12 см. Точка М не лежит в плоскости трапеции, а точка...

Question

В трапеции ABCD основание ВС равно 12 см. Точка М не лежит в плоскости трапеции, а точка К — середина отрезка ВМ. Докажите, что плоскость ADK пересекает отрезок МС в некоторой точке Н, и найдите отрезок КН.

Answer 1

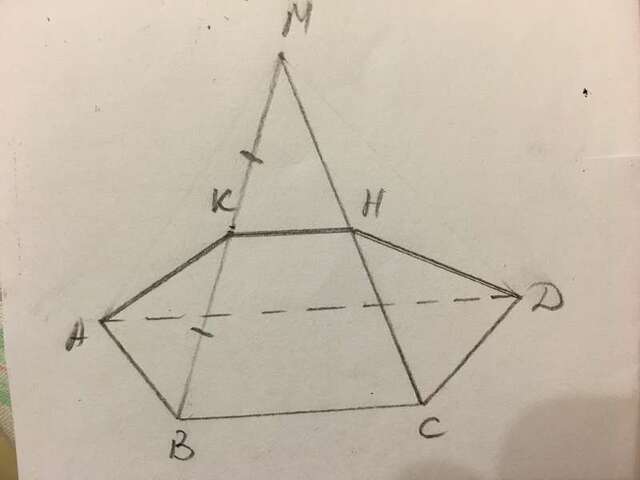
Прямые АК и ВМ пересекаются в точке К. АК∈АКД, ВМ∈ВМС, значит плоскости АКД и ВМС не параллельны, значит пересекаются. 
Плоскость АКД пересекает плоскость ВМС по прямой КН, ведь прямые АД и ВС, через которые проходят обе плоскости параллельны, а сами плоскости нет. При этом КН║АД и КН║ВС.
В тр-ке ВМС КН║ВС и ВК=КМ, значит КН - средняя линия. Точка Н∈МС.
Доказано.
КН=ВС/2=12/2=6 см - это ответ.

---

Comments

А можно поинтересоваться какой у вас был чертёж?

---

чертёж нарисовал "на коленке" - на клочке бумаги. проблема с чертежом? там ничего сложного.

---

Есть некоторые проблемы((

---

попробую набросать.

---

Спасибо))

---

Рад помочь.