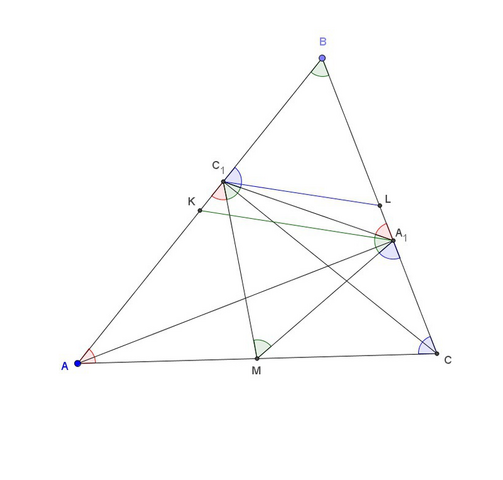
Т.к. AC₁C - прямоугольный, то MC₁=AM, т.е. ∠AC₁M=∠BAC и из подобия треугольников ABC и A₁BC₁ следует ∠A₁C₁B=∠ACB. Значит ∠MC₁A₁=180°-∠AC₁M-∠A₁C₁B=180°-∠BAC-∠ACB=∠ABC. Аналогично, ∠MA₁C₁=∠ABC. Т.к. по условию ∠C₁MA₁=∠ABC, то MA₁C₁ - равносторонний и ∠ABC=60°. Итак, из прямоугольности треугольника СС₁B и того, что ∠ABC=60° следует, что BL=C₁L=BC₁ и, аналогично, из прямоугольности треугольника AA₁B следует, BK=KA₁=BA₁. Значит, C₁K=BK-BC₁=BA₁-BL=A₁L, что и требовалось.