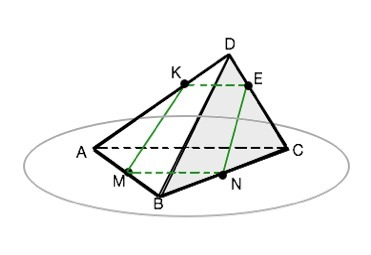
Пространственный четырехугольник - это выпуклый четырехугольник, "согнутый" по одной из диагоналей. При этом он похож на треугольную пирамиду без основания и одной из граней.
Через любые три точки можно провести плоскость. Точки А, В и С, как и точки А, D и C, определяют плоскости треугольников АВС и ADC.
По условию диагонали АС=ВD.
M и N середины АВ и ВС. ⇒ MN - средняя линия треугольника АВС, равна половине диагонали АС и параллельна ей. MN=AC:2
В ∆ АDC точка точка К не середина АD. Аналогично в ∆ BDC т.Е не середина DC. Поэтому КЕ не является средней линией ∆ ADC,
Из отношения DK:KA=DE:EC=1:2 следует подобие ∆ DKE и ∆ DAC.
k=AD:KD=3:1
КЕ║АС.
КЕ< 0,5АС и не равно MN
КЕ║А, MN║АС.
Если две прямые параллельны третьей прямой, то они параллельны. ⇒
КЕ||MN. ⇒
Четырехугольник MNEK – трапеция, что и требовалось доказать.