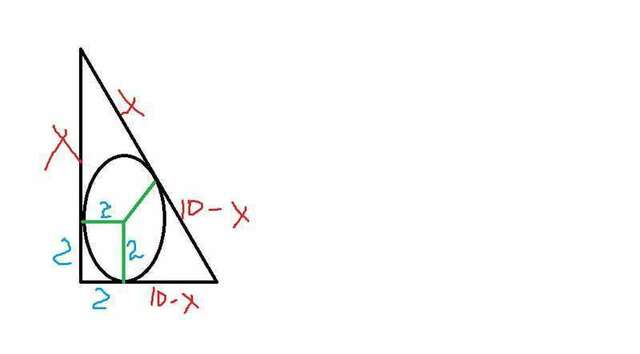
Радиус вписанной окружности, проведенный к точке касания перпендикулярен касательной.
Если из какой-нибудь точки (вершины треугольника) провести две касательные к окружности, то их отрезки от данной точки до точек касания равны между собой.
Обозначим один из отрезков х, тогда стороны треугольника будут
2+х
2+10-х
10
по т Пифагора
(2+х)²+(12-х)²=10²
4+4х+х²+144-24х+х²=100
х²-10х+24=0
х₁=4 х₂=6
Значит стороны равны 2+4=6 и 12-4=8
или 2+6=8 и 12-6=6
катеты 6 и 8
Площадь = 0,5*6*8=24
Ответ 24