В параллелограмме ABCD высота, опущенная из вершины тупого угла В делит сторону АD **...

0 голосов
80 просмотров

В параллелограмме ABCD высота, опущенная из вершины тупого угла В делит сторону АD на отрезки АК=64 см, КD=225 см. Найти длину диагонали ВD, если она перпендикулярна боковой стороне.

Геометрия (30 баллов) | 80 просмотров
Дан 1 ответ
0 голосов
Правильный ответ

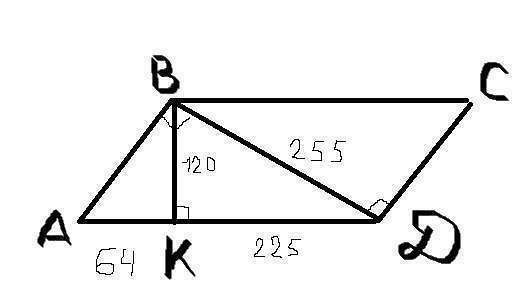
Дано: ABCD - параллелограмм. BK\perp AD, AK=64 см, KD=225 cм, BD\perp DC.

 

Найти: BD

 

Решение: Треугольник АВD является прямоугольным, так как BD перпендикулярно DC. A DC||AB. Значит BD является секущей при параллельных АВ и CD. Поэтому

\angle ABD=\angle BDC=90^\circ

 

Есть такое свойство в прямоугольном треугольнике, что высота, проведенная к гипотенузе, является средним геометрическим отрезков, на которое делит высота гипотенузу.

 

BK=\sqrt{AK*KD}=\sqrt{64*225}=\sqrt{8^2*15^2}=8*15=120

 

BK=120 см.

 

Теперь по теореме Пифагора BD - гипотенуза треугольника BKD.

 

BD^2=BK^2+KD^2

 

BD=\sqrt{BK^2+KD^2}=\sqrt{120^2+225^2}=

 

=\sqrt{(3*2^3*5)^2+(3^2*5^2)^2}=\sqrt{3^2*2^6*5^2+3^4*5^4}=

 

\sqrt{3^2*5^2*(2^6+3^2*5^2)}=3*5*\sqrt{2^6+15^2}=15\sqrt{64+225}=

 

=15\sqrt{289}=15*17=255

 

Ответ: BD=255 cм.

image
(114k баллов)
Похожие задачи