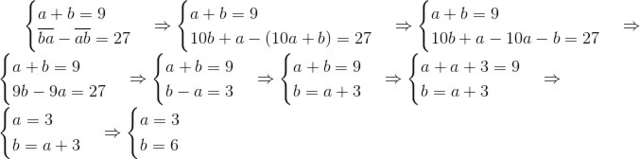Пусть  , где
, где  — цифра, стоящая в разряде десятков,
— цифра, стоящая в разряде десятков,  — цифра, стоящая в разряде единиц, — наше двузначное число. Тогда, по условию,
— цифра, стоящая в разряде единиц, — наше двузначное число. Тогда, по условию,  . А число, записанное теми же цифрами, но в обратном порядке, —
. А число, записанное теми же цифрами, но в обратном порядке, —  . По условию,
. По условию,  . Отсюда система уравнений:
. Отсюда система уравнений:
см. приложение.
Ответ:  .
.