Основы трапеции равны 3 см и 19 см, а диагонали- 16 см и 8 см. Найдите площадь трапеции.

0 голосов
13 просмотров

Основы трапеции равны 3 см и 19 см, а диагонали- 16 см и 8 см. Найдите площадь трапеции.

Геометрия (18 баллов) | 13 просмотров
Дано ответов: 2
0 голосов

Я достроил трапецию до другого четырехугольника, постоив из вершины нижнего основания сторону, парвлельную диагонали 8 см. Получилось два подобных треугольника. Нахожу косинус желтого угла:
22^2=16^2+8^2-2*8*16*cos\alpha;\\ 484=256+64-256*cos\alpha;\\ 164=-256*cos\alpha;\\ cos\alpha=-\frac{164}{256}=-\frac{41}{64};\\ cos\beta=cos(180-\alpha)=-cos\alpha=\frac{41}{64};\\ sin\beta=\sqrt{1-\frac{1681}{4096}}=\sqrt{\frac{2415}{4096}}=\frac{\sqrt{2415}}{64};\\ S=\frac{8*16*sin\beta}{2}=\sqrt{2415};\\

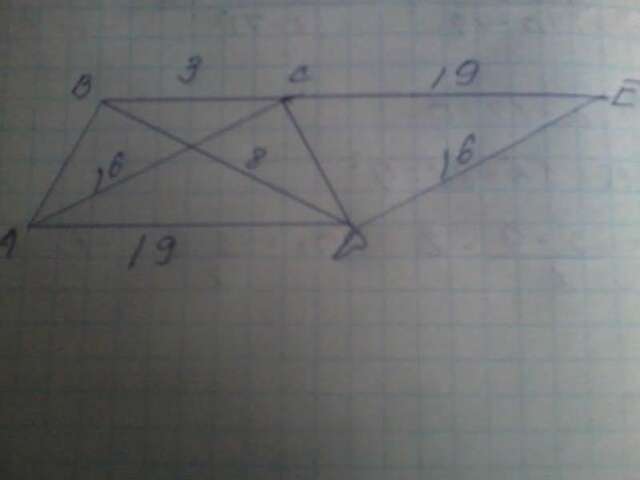
image
(1.7k баллов)
0 голосов

рисунок во вложении

Продолжим ВС вправо на длину нижнего основания

Соеденив получившуюся точку Е с D получим треугольник со сторонами 22,16,8

Найдем по формуле Герона площадь этого треугольника  

Потом вычесляем высоту трапеции и площадь ее. 

Во вложении

 

image
image
(1.8k баллов)
Похожие задачи