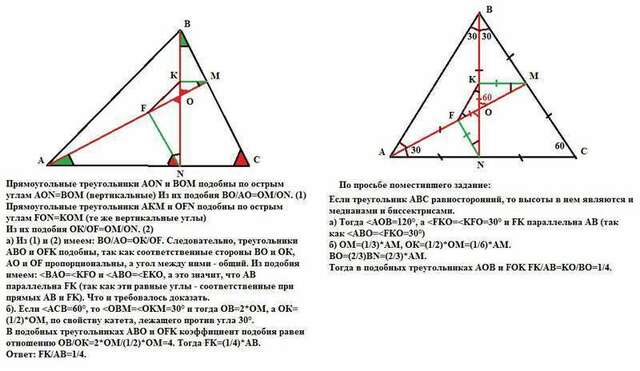
В ΔАВС проведены высоты АМ и BN. На них из точек M и N опущены перпендикуляры МК и NF соответственно.
а) Докажите, что АВ и КF параллельны
б) Найдите отношение KF:AB если <АСВ=60°.<br>
Прямоугольные треугольники АОN и ВОМ подобны по острым углам АОN=ВОМ (вертикальные). Из их подобия ВО/АО=ОМ/ON. (1)
Прямоугольные треугольники АКМ и OFN подобны по острым углам FОN=KОМ (те же вертикальные углы).
Из их подобия ОК/ОF=ОМ/ON. (2)
Значит ВО/АО=ОК/ОF. Следовательно, треугольники АВО и OFK подобны, так как соответственные стороны ВО и ОК, АО и OF пропорциональны, а угол между ними - общий.
Из подобия имеем: что АВ параллельна FK (так как эти равные углы - соответственные при прямых AB и FK). Что и требовалось доказать.
б). Если В подобных треугольниках АВО и OFK коэффициент подобия равен отношению ОВ/ОК=2*ОМ/(1/2)*ОМ=4. Тогда FK=(1/4)*АВ.
Ответ:KF/AB=1/4.