Одна из диагоналей параллелограмма равна 3√6 и образует с основанием угол 60°.
Найти длину второй диагонали, если она образует с основанием угол 45°.
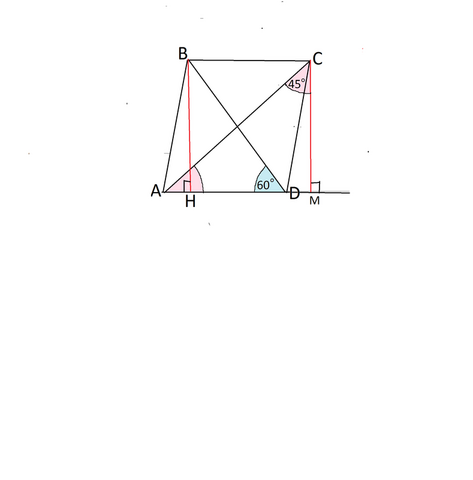
На рисунке ВD - диагональ, длина которой 3√6.
Угол ВDА =60°.
Диагональ АС образует с тем же основанием угол САD, равный 45°.
Опустим из В на основание АD высоту ВН.
ВН =ВD*sin(60°)
ВН= 3√6√3):2=3√18):2=9√2):2
Из вершины С опустим перпендикуляр на продолжение АD.
Получили прямоугольный равнобедренный треугольникСDА, в котором катеты
CМ =АМ = 9√2):2
АС в нем - гипотенуза.
АС=СМ√2=9√2*√2):2=9