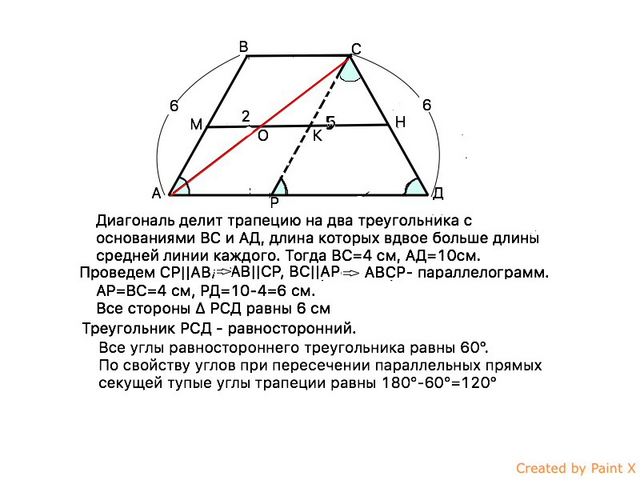
Диагональ делит трапецию на два треугольника с основаниями ВС и АД, длина которых вдвое больше средней линии каждого треугольника. Тогда ВС=4 см, АД=10 см.
Проведем СР||АВ
Противоположные стороны четырехугольника АВСР параллельны.
АВСР - параллелограмм, ВС=АР=4 см, и СР=АВ=6 см
РД=АД-АР=10-4=6 см
Все стороны треугольника РСД равны.
Треугольник РСД - равносторонний.
Все углы равностороннего треугольника равны 60°.
∠ ВСР=∠ВАР=60°
∠ВСД=СВА=60°+60°=120°
Углы при каждом из оснований равнобедренной трапеции равны.
Острые углы данной трапеции равны 60°, тупые - 120°.