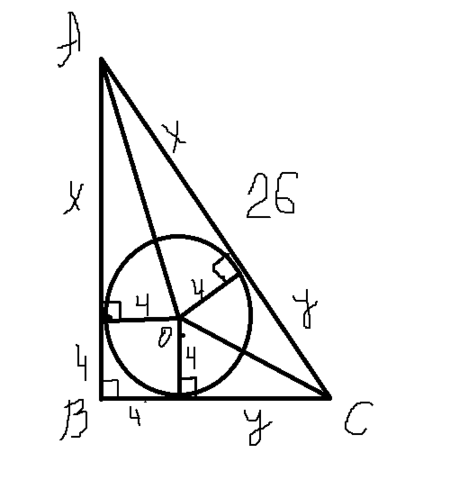Рассмотрим прямоугольный треугольник АВС с прямым углом В. Пусть точка О - центр вписанной окружности. Проведем из точки О радиусы в точки касания вписанной окружности со сторонами треугольника. Назовем основания этих радиусов М, N, K. Эти радиусы будут перпендикулярны к сторонам треугольника(свойство радиуса, проведенного в точку касания). Соединим также точку О с вершинами А и С треугольника.
Теперь рассмотрим четырехугольник ВМОК: очевидно, что это квадрат со стороной 4 см.
Рассмотрим треугольники АМО и АNО: они прямоугольные и равны по катету и гипотенузе( АО-общая гипотенуза, МО=ОN=4) Из равенства треугольников следует, что АМ=AN. Обозначим длины этих сторон за х.
Аналогично доказываем, что СК=СN. Обозначим их за у.
Периметр треугольника будет равен 2х+2у+8= 2(х+у)+8. Так как х+у=26, то Р= 2*26+8=60.
Ответ:60см ( Рисунок во вложении. )