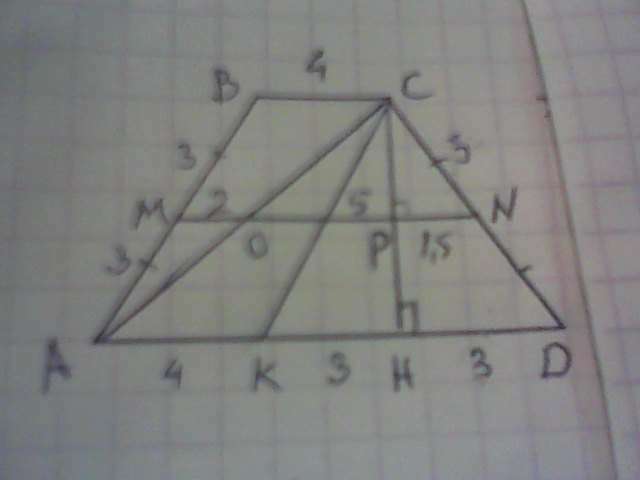
Дано: АВСD - равнобокая трапеция, АВ=СD= 6 см, МN- средняя линий,
МО= 2 см; ОN=5 см.
Найти: ∠ВАD, ∠АВС
Решение.
ΔАВС. ОМ- средняя линия, равна 2 см, значит ВС=4 см., средняя линия в 2 раза меньше ВС.
ΔАСD. ОN- средняя линия равна 5 см. значит АD= 10 см.Построим СК║АВ. АВСК - параллелограмм, противоположные стороны параллельны и равны: АК=ВС=4 см.СК=АВ=6 см.
ΔСDК равнобедренный: СК=СD= 6 см.
Построим СН⊥АD, тогда КD=АD-АК=10-4=6 см. Но СН также является медианой в равнобедренном ΔКСD, значит КН=НD=6/2=3 см.
ΔСDН. cosD=HD/CD=3/6=0,5. ∠НDС=60°. ∠ВАD=СDА=60°.
∠АВС=∠ВСD=180-60=120°.
Ответ: 60°; 120°.