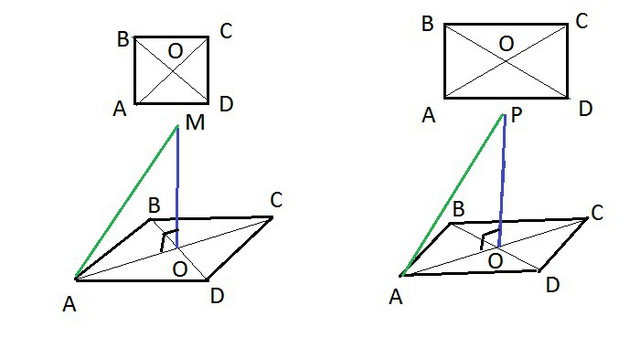
1) Равные наклонные имеют равные проекции.
АО=ВО=ОС=ОD
По теореме Пифагора из треугольника АВС
АС²=АВ²+ВС²=(6√2)²+(6√2)²=72+72=144
АС=12
АО=6
По теореме Пифагора из треугольника МАО
МО²=МА²-АО²=10²-6²=64
МО=8
2) Пусть АВ=2х; ВС=3х, тогда АВ:ВС=2:3
Р=2·(2х+3х)=10х
10х=40
х=4
АВ=8;
ВС=12
Равные наклонные имеют равные проекции.
АО=ВО=ОС=ОD
По теореме Пифагора из треугольника АВС
АС²=АВ²+ВС²=(8)²+(12)²=64+144=208
АС=√208=4√13
АО=√208/2=2√13
По теореме Пифагора из треугольника РАО
РО²=РА²-АО²=14²-(2√13)²=196-52=144
РО=12