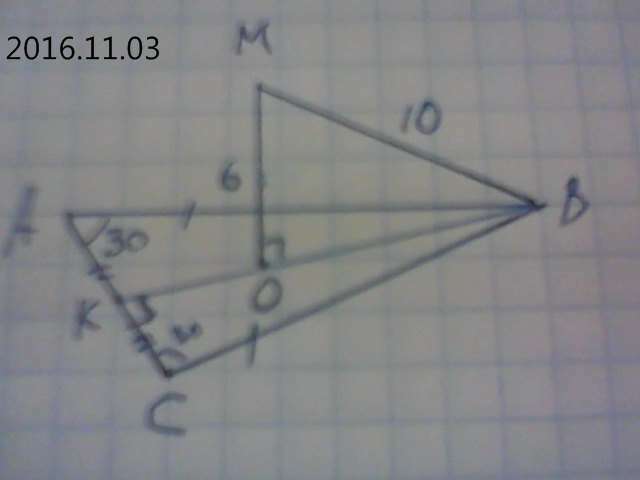
1) см. рис. ΔОМВ- прямоугольный (МОВ=90°). ОВ²=ВМ²-ОМ²=100-36=64,
ОВ=√64=8 см.
ΔАВК=ΔСВК. АВ=ВС ( по условию), ∠ВАК=∠ВСК =30° (углы при основании в равнобедренном треугольнике равны), ВК =общая сторона. Значит АК=ВК. ВК -медиана. биссектриса и высота одновременно.
∠АВС=180°-30-30=120°.
ΔВСК. ∠СВК=90-30=60°. Точка О делит ВК в отношении 2 : 1, значит ВО=8, ОК=4, ВК=8+4=12.
Пусть СК=х, ВК лежит против угла 30°. равен половине гипотенузы, ВК=12 см, ВС=2·12=24 см.
АВ=ВС=24 см
ΔВСК. СК²=ВС²-ВК²=576-144=432.
СК=√432=12√3 см.
Ответ: 24 см, 24 см, 12√3 см.
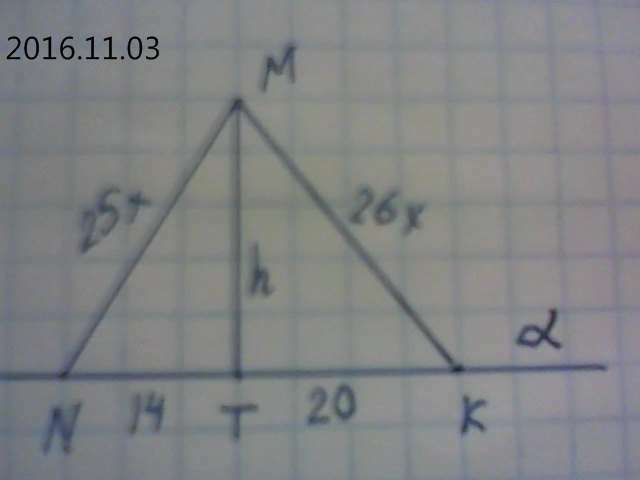
2) см.рис. Плоскость изображена в виде прямой α.
Пусть одна часть равна х, тогда по условию МN=25х, МК=26х. Обозначим МN=h.
ΔМNТ. h²=МN²-NТ²=625х²-196.
ΔМКТ. h²=МК²-ТК²=676х²-400,Правые части обоих равенств равны:
676х²-400=625х²-196,
676х²-625х²=400-196,
51х²=204,
х²=204/51=4,
х=√4=2 см.
Есть возможность найти h.
h²=625·4-196=2304,
h=√2304=48 см.
Ответ: 48 см.