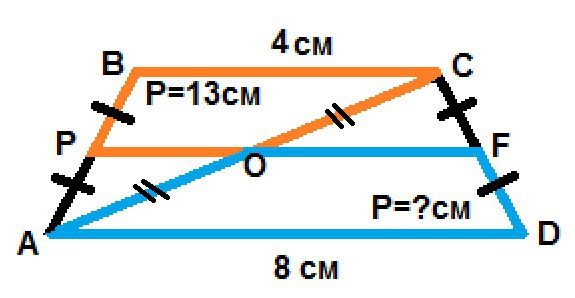
Дано: равнобедренная трапеция ABCD, P - середина AB, F - середина CD,
BC = 4см, AD = 8см, периметр трапеции OPBC = 13см.
Найти: периметр трапеции AOFD.
Решение.
1) PF - средняя линия трапеции → PO = BC/2 = 4см/2 = 2см, OF = AD/2 = 8см/2 = 4см
2) Периметр OPBC(13см) = OP(2см)+PB+BC(4см)+CO → PB+CO = 13см-6см = 7см
3) PB=FD, т.к. средняя линия PF соединяет середины боковых сторон в равнобедренной трапеции; CO=AO, т.к. средняя линия PF делит диагональ AC на равные отрезки по теореме Фалеса →
Периметр AOFD = (FD+AO)(7см)+OF(4см)+DA(8см) = 19см
Ответ: 19см.