Y=x^2-7x+10 Построить график

$f(x) = x^2-7x+10$ - сразу заметим, что графиком данной функции будет парабола, ветви направлены вверх, т.к. коэффициент при старшей степени переменной - положителен (равен 1)
1. Решим вспомогательное уравнение:
$x^2-7x+10=0$
$D= 7^2-4*10*1 = 49-40=9$
$x_{1}= \frac{7-3}{2} =2$
$x_{2}= \frac{7+3}{2} =5$
Точки $x_{1}$ и $x_{2}$ - нули функции. В данных точках график пересекает ось оХ.
2. Найдем вершину параболы:
$(- \frac{b}{2a} ; - \frac{b^2-4ac}{4a} )$ , где $- \frac{b}{2a}$ ∈ оси oX, а $- \frac{b^2-4ac}{4a}$ ∈ оси оY.
$- \frac{-7}{2} = \frac{7}{2} =3,5$
$- \frac{49-40}{4}= \frac{9}{4} =-2,25$
итак, координаты вершины:
$(3,5; -2,25)$
3. Найдем значение функции в некоторых точках:
f(1) = 1-7+10=4
f(-1)= 1+7+10=18
f(6) = 36-42+10 = 4
f(-4) = 14+28+10 = 54
*подставляем выбранный иск в формулу

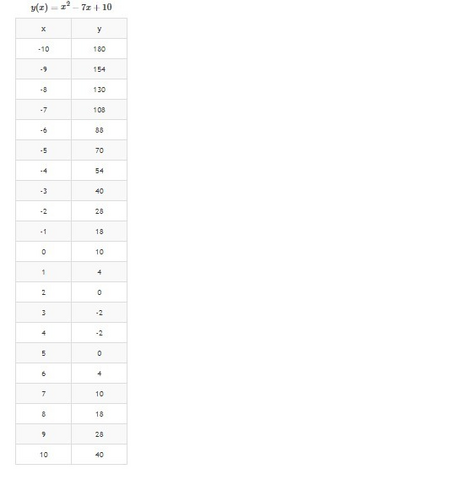
График и полная таблица точек для построения представлены во вложениях: