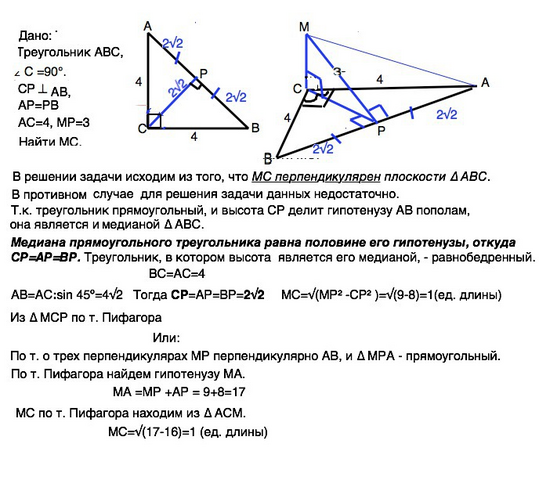
Дано: Треугольник АВС, ∠ С - прямой.
СР - перпендикулярно АВ,
АР=РВ
АС=4, МР=3
Найти МС.
В решении задачи исходим из того, что МС перпендикулярен плоскости ∆ АВС.
Т.к. треугольник прямоугольный, и высота СР делит гипотенузу АВ пополам, она является и медианой ∆ АВС.
Медиана прямоугольного треугольника равна половине его гипотенузы, откуда СР=АР=ВР. Треугольник, в котором высота является его медианой, - равнобедренный.
ВС=АС=4
АВ=АС:sin 45º=4√2
Тогда СР=АР=ВР=2√2
Из ∆ МСР по т. Пифагора
МС=√(МР² -СР² )=√(9-8)=1(ед. длины)
Или:
По т. о трех перпендикулярах МР перпендикулярно АВ, и ∆ МРА - прямоугольный.
По т. Пифагора найдем гипотенузу МА.
МА =МР +АР = 9+8=17
МС по т. Пифагора находим из ∆ АСМ.
МС=√(17-16)=1 (ед. длины)