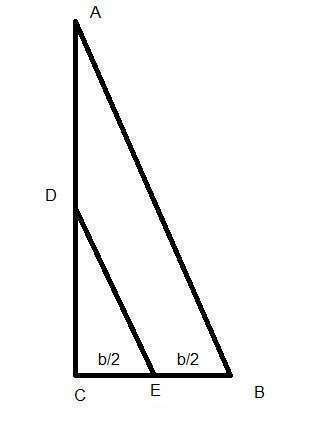
Бо'льшая ср линия треуг-ка, параллельна большей стороне прямоуг тег-ка, т.е. гипотенузе.Т.е. необходимо найти DE
Меньший катет лежит против меньшего угла CAB, следовательно больший угол CBA(т.е тот который больше другого острого угла) лежит против большего катета.
Пусть угол CAB=x
Тогда угол ABC=x+a
Т.к. сумма углов треуг-ка равна 180, а угол АСВ=90, легко вычислить, что
угол CAB=180-90-(x+a)
x=180-90-x-a
2x=90-a
x=(90-a)/2
Далее необходимо доказать подобие треуг-ков ACB и DCE
Т.к треуг ACB и DCE подобны, то угол BAC=углу EDC
ED=EC*sin угла CDE = b/2 *sin ((90-a)/2)