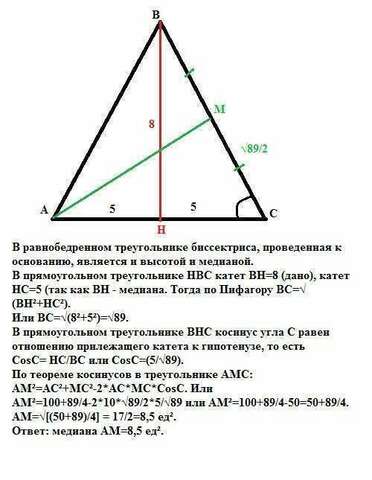
Проведем медиану АМ к боковой стороне ВС.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является и высотой и медианой.
В прямоугольном треугольнике НВС катет ВН=8 (дано), катет НС=5 (так как ВН - медиана. Тогда по Пифагору BC=√(BH²+HC²).
Или ВС=√(8²+5²)=√89. Тогда МС=√89/2, так как АМ - медиана.
В прямоугольном треугольнике ВНС косинус угла С равен отношению прилежащего катета к гипотенузе, то есть
CosC= НС/ВС или CosC=(5/√89).
По теореме косинусов в треугольнике АМС:
АМ²=АС²+МС²-2*АС*МС*CosC. Или
АМ²=100+89/4-2*10*√89/2*5/√89 или АМ²=100+89/4-50=50+89/4.
АМ=√[(50+89)/4] = 17/2=8,5 ед².
Ответ: медиана АМ=8,5 ед².