Если бы никакого препятствия в виде стены не было, то уравнения движения маятника для угла и двух его производных от времени выглядело бы так:
φ = Φcosωt (Φ – начальное и максимальное значение угла отклонения) ;
φ' = –Φωsinωt ;
φ'' = –Φω²cosωt ;
В нашем случае, во время столкновения – всё пойдёт немного не так, но поскольку вне стены маятник предоставлен сам себе, а после упругого столкновения полная энергия, а значит и амплитуда колебаний сохраняется, то вне стены он будет продолжать колебаться как маятник. Уравнение движения в таком случае можно записать так:
φ = Φcosδ ;
φ' = –Φωsinδ ;
φ'' = –Φω²cosδ ;
Где внутренний гармонический параметр δ – или «фаза» будет уже зависеть от времени не просто линейно, а как-то сложнее. Разберёмся с этим.
До первого столкновения со стенкой колебание не отличается от обычного гармонического, а значит δ = ωt ;
Не указано, как сориентирована стенка, т.е. идёт ли она круто под наклоном, так что свободно мятник на ней просто лежит, или же стенка вообще отвесная, и маятник может висеть рядом с ней вертикально. Так что величина угла столкновения может быть, как Φ/2, так и –Φ/2 (для отвесной стенки):
Итак, когда грузик достигнет стены: φ = ±Φ/2, получаем:
±Φ/2 = Φcosδн ;
cosδн = ±1/2 ;
δн+ = π/3 – фаза начала удара для крутой стенки, на которой свободный маятник лежит;
δн– = 2π/3 – фаза начала удара для отвесной стенки с возможностью вертикального провисания;
После удара об стену, грузик изменит свою угловую скорость φ' – на противоположную, а отклонение φ и ускорение φ'' (определяемое только отклонением φ) останется таким же. При этом произойдёт какой-то скачок «фазы» δ, с фазы начала удара δн до фазы конца удара δк
φ(δк) = φ(δн) ;
φ'(δк)=–φ'(δн) ;
φ''(δк) = φ''(δн) ;
cosδк = cosδн ;
–sinδк = sinδн ;
–cosδк = –cosδн ;
cosδк = cos[–δн] ;
–sinδк = –sin[–δн] ;
δк = –δн ;
Учитывая фазу начала удара, получаем фазу окончания удара:
δк+ = –π/3 – фаза окончания удара для крутой стенки, на которой свободный маятник лежит;
δк– = –2π/3 – фаза окончания удара для отвесной стенки с возможностью вертикального провисания;
Рассмотрим первый случай крутой стенки, где фаза при ударе делает скачок от δн+ = π/3 до δк+ = –π/3 .
После скачка фазы с π/3 до –π/3 опять будет происходить обычное колебание до фазы π/3 начала следующего удара.
Есть прекрасная функция, которая монотонно растёт, а потом срывается вниз и опять проходит те же значения каждый отрезок длиной в π. Это функция тангенса. Только она растён НЕ на интервале ( –π/3 ; π/3 ), а на в 1.5 раза более широком. Ок. Сузим интервал внутеренним аргументным коэффициентом и возьмём от этого всего уже не периодический арктангенс. Тогда получится, что:
δ = [2/3] arctg tg ( [3/2] ωt ), в самом деле:
От ωt=0 нуля до ωt=π/3 функция δ = [2/3] arctg tg ( [3/2] ωt ) = ωt ,
Затем происходит скачок и [2/3] arctg даёт уже значения фазы на на [2/3] π меньшие, что как раз соответствует необходимому скачку.
Тогда уравнение колебания данной системы можно записать, как:
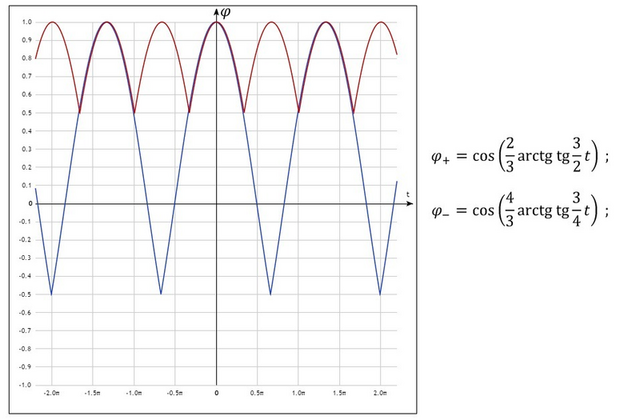
φ+ = Φcos ( [2/3] arctg tg ( [3/2] ωt ) ) ;
Аналогично можно показать, что для отвесной стены уравнение запишется, как:
φ– = Φcos ( [4/3] arctg tg ( [3/4] ωt ) ) ;
Смотрите иллюстрацию:
Период в обоих случаях определяется внутренней периодической функцией тангенса:
ОТВЕТ:
T+ = π/([3/2]ω) = [2π/3] √[L/g] – для крутой стенки, на которой свободный маятник лежит;
T– = π/([3/4]ω) = [4π/3] √[L/g] – для отвесной стенки с возможностью вертикального провисания.