В прямоугольных треугольниках АМО и СМО
АО=ОС=a√3.
МО- общая ⇒ МА=МС
Но данных недостаточно, нужны две величины.
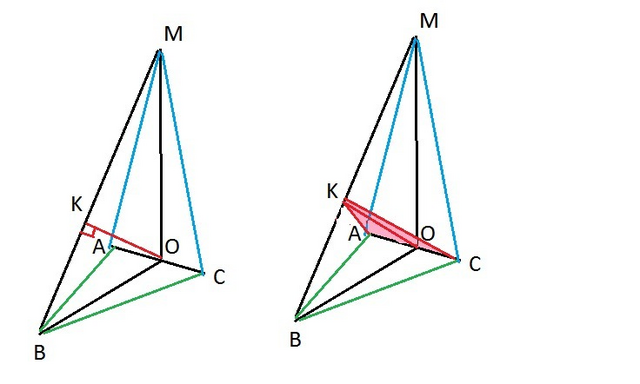
В прямоугольном треугольнике ВМО высота ОК, проведенная из вершины прямого угла равна расстоянию от точки О до прямой ВМ.
ОК=а.
других данных нет.
∠СКА - линейный угол двугранного угла между плоскостями (AMB) и (CMB)
, так как по теореме о трех перпендикулярах.
АК⊥ВМ
СК⊥ВМ