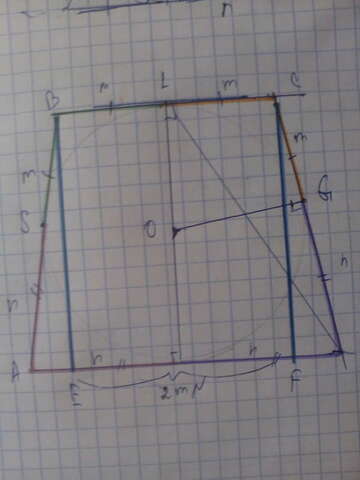
Раз в трапецию можно вписать окружность, то суммы противоположных её сторон равны.
BC = CM = LB = BN и BS = SA = AN = ND = DG, т.к трапеция равнобоковая и отрезки касательных, проведённые из одной точки равны.
Опустим два перпендикуляра к большему основанию AD. Обозначим их за BE т FC. Внутри трапеции образовался прямоугольник BEFC => BC = EF = 2m. Тогда AE + FD = 2n - 2m.
AB = CD
BE = CF
Угол AEB = углу DFC = 90°
Значит, треугольник равны по катеты и гипотенузе.
Из равенства треугольников => AE = FD. Значит, AE = FD = 1/2(AE + FD) = 1/2•(2n - 2m) = n - m.
По теореме Пифагора:
BE = √(m + n)² - (n - m)² = √m² + 2mn + n² - n² + 2mn - m² = √4mn = 2√mn.
Значит, высота трапеции равна 2√mn.
Площадь S трапеции равна:
S = 1/2(BC + AD)•EB
S = (m + n)•2√mn.