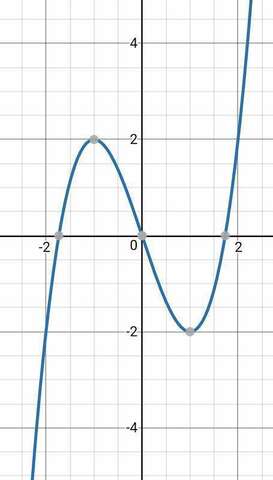
F(x)=x^3-3x;
1) ищем 1 и 2 производную:
f(x)'=3x^2-3;
f(x)''=3(2x)=6x;
2) ищем критические точки:
3x^2-3=0; x^2=1; x1=1; x2=-1;
y1=-2; y2=2; (1;-2) и (-1;2);
3) возрастание/ убывание, точки минимум/максимум и экстремиумы:
методом интервалов определяем где производная менят знак и находим:
убываеи: x=[-1;1]
возрастает: x=(-беск;-1] и [1;+беск)
экстремиумы: (1;-2) и (-1;2)
минимум: x=1
максимум: x=-1
4) т.к D(f(x))=R, асимтот не имеет;
5) f(-x)=(-x)^3-3(-x)=-x^3+3x=-(x^3-3x)=-f(x) - функция нечетная;
6) ищем выпуклости/вогнутости:
для этого используем 2 производную:
6x=0; x=0;
y=0;
выпуклая: (-беск;0]
вогнутая: [0;+беск]
7) берем еще пару точек и строим график