ДАНО
Y = x²/(x-1)
ИССЛЕДОВАНИЕ
1) Область определения - непрерывность функции.
Разрыв при Х=1.
Х∈(-∞;1]∪[1;+∞)
2) Пересечение с осью Х - Х=0.
3) Пересечение с осью У - У(0) = 0.
4) Поведение в точке разрыва.
У(1+) = +∞ и У(1-) = -∞
5) Поведение на бесконечности
У(+∞) = +∞ и У(-∞) = -∞.
6) Наклонная асимптота - У = Х+1
7) Исследование на чётность.
У(х) = х²/(х-1)
У(-х) = - х²/(х+1)
Функция ни чётная ни нечетная.
8) Производная функции
У' = 2x/(x-1) - x²/(x-1)²
9) Корни производной - точки экстремумов.
х1 = 0 - максимум - У(0) = 0
х2 = 2 - минимум - У(2) = 4
10) Монотонность функции.
Возрастает - У∈(-∞;0]∪[2;+∞)
Убывает - У∈[0;1)∪(1;2]
11) Выпуклая - Х∈(-∞;1) и вогнутая - Х∈(1;+∞).
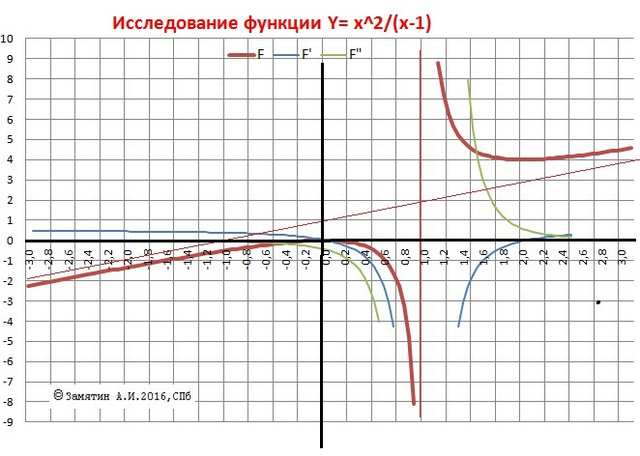
12) График функции и производных прилагается.