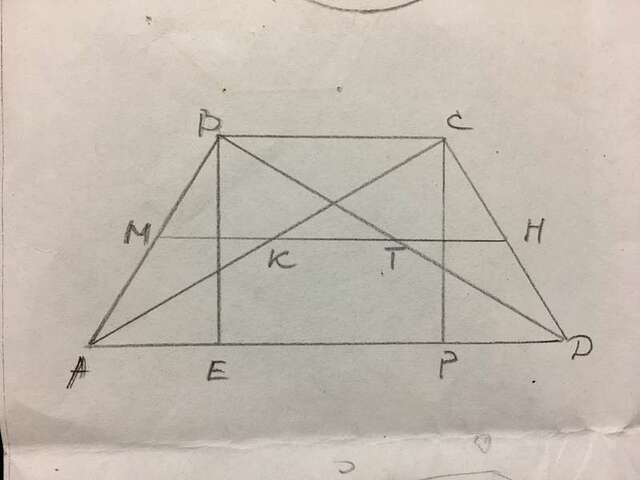
Так как углы А и Д равны, то трапеция равнобедренная.
По услови МТ-ТН=8 см.
МК=ТН, значит КТ=МТ-МК=8 см.
ВЕ и СР - высоты к основаниям трапеции.
В равнобедренной трапеции отрезки АЕ и РД равны, т.к. равны тр-ки АВЕ и ДСР (АВ=СД, ∠А=∠Д и оба прямоугольные). АЕ=РД=(АД-ВС)/2.
В тр-ках АВС и ДВС отрезки МК и ТН равны и являются средними линиями. МК=ТН=ВС/2.
КТ=МН-(МК+ТН)=[(АД+ВС)/2]-BC=(АД-ВС)/2, значит АЕ=РД=КТ=8 см.
В прямоугольном тр-ке АВЕ ∠АВЕ=90-∠ВАЕ=90-60=30°, значит АВ=2АЕ=16 см.
Периметр трапеции: Р=2АВ+2ВС+2АЕ ⇒⇒ ВС=(Р-2(АВ+АЕ))/2,
ЕР=ВС=(72-2(16+8))/2=12 см,
АД=ЕР+2АЕ=12+2·8=28 см - это ответ.