Не очень уверен в вычислениях
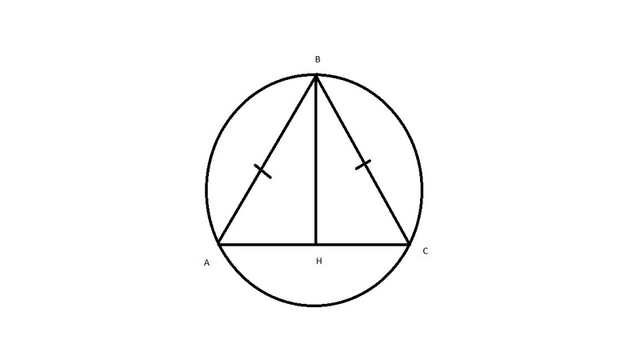
Проведем в треугольнике ABC высоту BH (она является еще и медианой, биссектрисой, т.к. треугольник равнобедренный).
Углы треугольника при основании (180/120)/2=30 гр.
Рассмотрим прямоугольный треугольник ABH. Катет BH лежит против угла в 30 гр. значит он равен 1/2*5=2,5. По теореме Пифагора найдем второй катет AH=√5^2-2,5^2=√25-6,25=√18,75=(5√3)/2
Диаметр описанной окружности равен 2S/p, где S-площадь, а p-полупериметр.
Площадь треугольника равна 2,5*2*(5√3)/2/2=6,25√3
Полупериметр равен (5+5+5√3)/2=10+5√3/2
d=2*6,25√3/10+5√3/2=10√3-15