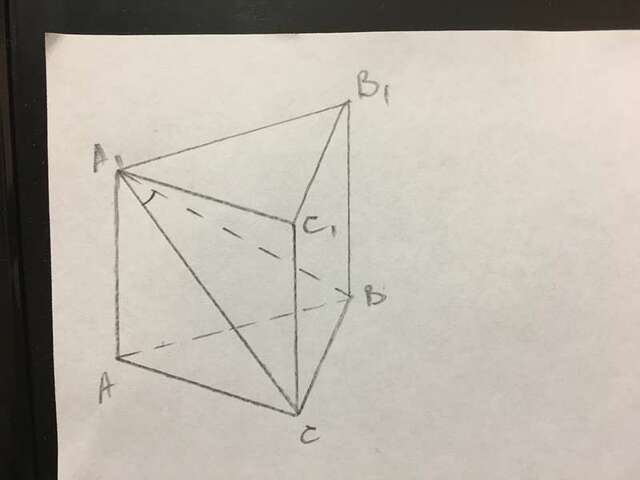
В призме АВСА1В1С1 все боковые грани - квадраты, значит все рёбра призмы равны.
А1В и А1С - пересекающиеся рёбра боковых граней. А1В=А1С.
Пусть боковое рёбро призмы равно а.
В квадрате АА1С1С диагональ А1С=а√2.
В тр-ке А1ВС по теореме косинусов cos(∠BA1C)=(А1В²+А1С²-ВС²)/(2А1В·А1С)=(2а²+2а²-а²)/(2а√2·а√2)=3а²/4а²=3/4=0.75.
∠ВА1С=arccos(3/4)≈41.4° - это ответ.