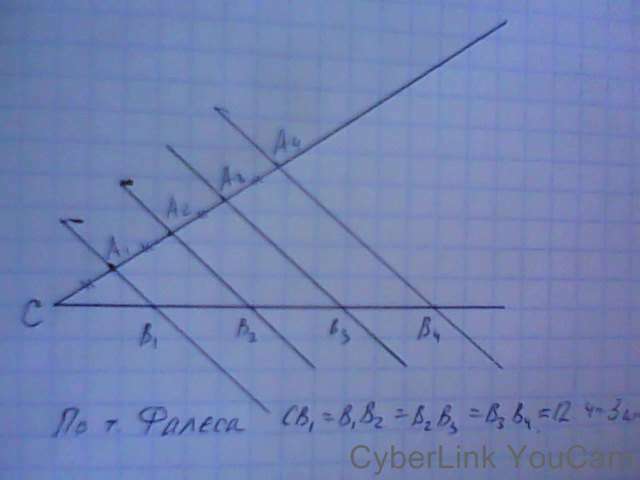
1) По теореме Фалеса СВ4 разделен на 4 равных отрезка, каждый из которых равен 32/4=8 см. В1В2=8 см; В2В4=2·8=16 см.
Пусть СА1=А1А2=А2А3=А3А4=х. Пусть ∠С=α.
Запишем площадь ΔСА4В4=S1.= 32 см².СА4=4х
S1=0,5·СА4·СВ4·соsα.
0,5·12·4х·соsα=32,
24х·соsα=32,
х·соsα=4/3.
S(СА3В3)=0,5·СА3·В3=0,5·3х·24·соsα=36х·соsα=36·4/3=48 см².
Ответ: 8 см; 16 см; 48 см².
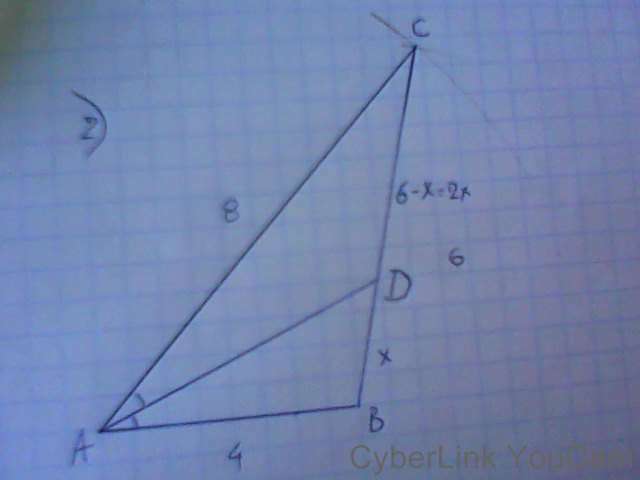
2) По свойству биссектрисы АВ : АС = ВD : СD;
4 : 8=х : 2х, отсюда ВС= х+2х=6; 3х=6; х=2.
СD=2 см, ВD=2·2=4 см.
Площадь ΔАВС найдем по формуле Герона
р=0,5(4+6+8)=9.
S(АВС)=√р(р-а)(b)(р-с)=√9·1·3·5=√135.
Про формуле Лагранжа АD²=АВ·АС-ВD·СD=4·8-2·4=32-8=24.
АD=√24 см.
S(АВD) по формуле Герона равна 3,87 см²
S(АВС)/S(АВD)=√135/3,87≈3.
Ответ: 2см; 4 см; 3.