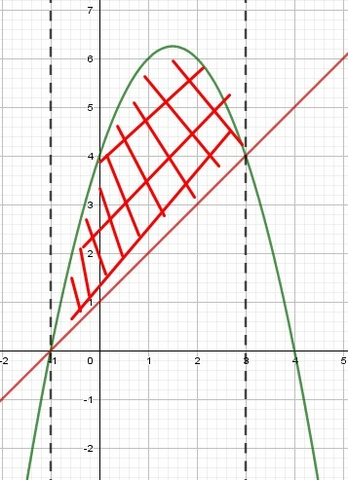
Графиком функции f(x)=y=-x²+3x+4 является парабола, ветви направлены вниз
m=-b/2a = -3/(2*(-1)) = 3/2 = 1.5
y = -1.5² + 3*1.5 + 4 = 6.25
(1.5; 6.25) - координаты вершины параболы.
g(x)=y=x+1 - прямая, которая проходит через точки (-1;0), (0;1)
Поскольку f(x)>g(x), то площадь ограниченной линиями равна: