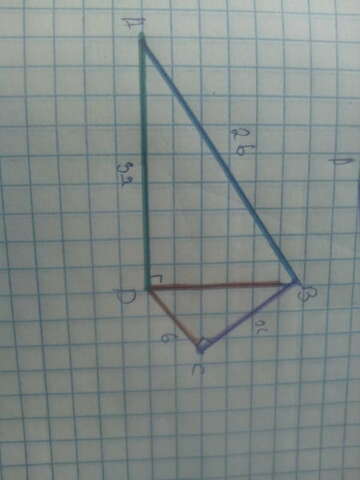
Дан четырёхугольник ABCD. Угол ∠С = 90°, а также диагональ BD перпендикулярна стороне AD.
Известно, что сторона AD в три раза больше стороны BC, а столоны AB и DC равны соответственно 26 см и 6 см. Найдите диагональ BD.
Решение:
Пусть BC = x. Тогда AD = 3x.
По теореме Пифагора:
BD² = 26² - (3x)²
BD² = 6² + x²
676 - 9x² = 36 + x²
640 = 10x²
x² = 64
x = 8
Значит, BC = 8 см.
По теореме Пифагора:
BD = √BC² + BD² = √8² + 6² = √64 + 36 = √100 = 10 см.
Ответ: 10 см.