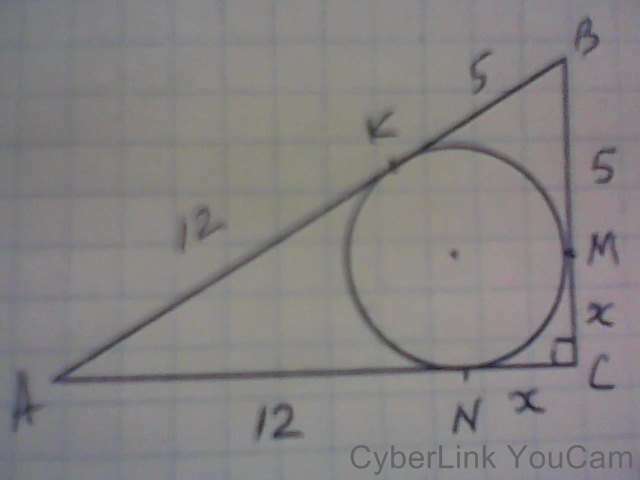
См.фото.
Точки касания окружности со сторонами треугольника АВС: К, М, N.
АК=АN=12 см; ВК=ВМ=5 см; СК=СМ=х.
АВ=АК+ВК=12+5=17 см,
ВС=5+х,
АС=12+х.
По теореме Пифагора АВ²=АС²+ВС²,
17²=(5+х)²+(12+х)²,
25+10х+х²+144+24х+х²=289,
2х²+34х+120=0, сократим на 2,
х²+17х-60=0,
х1=6; второй корень отрицательный, не удовлетворяет условию задачи.
АС=12+6=18 см,
ВС=5+6=11 см.
Ответ: 18 см, 11 см.