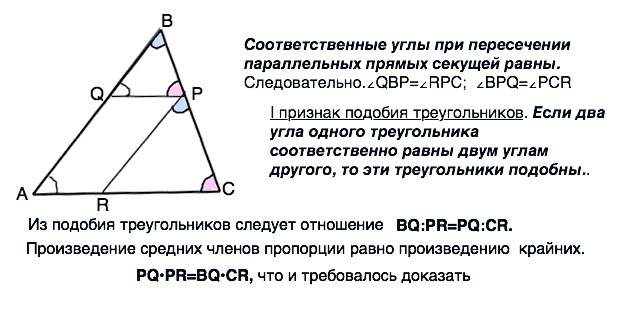
Соответственные углы при пересечении параллельных прямых секущей равны. Следовательно.∠QBP=∠RPC; ∠BPQ=∠PCR
I признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны.
Из подобия треугольников следует отношение
ВQ:PR=PQ:CR.
Произведение средних членов пропорции равно произведению крайних. PQ•PR=BQ•CR, что и требовалось доказать.