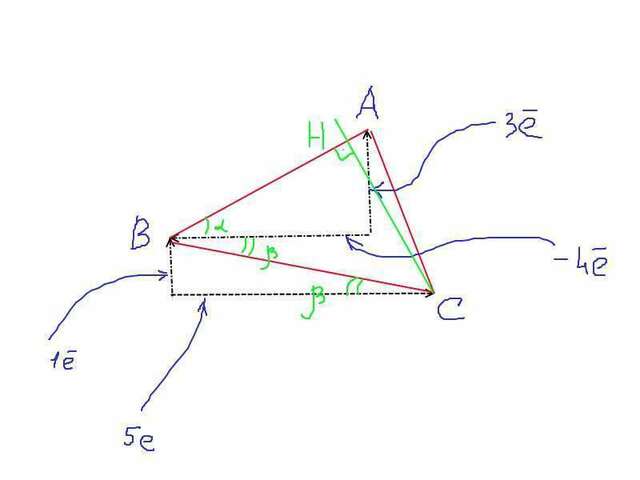
Нужно сначала построить треугольник АВС; строится он по единичным векторам (ортам), сначала строится АВ: по векторам 3е1-4е2; по сути это маленький прямоугольный треугольник с катетами 3е1 и -4е2; т.е. АВ - гипотенуза и равна она
5е1 или 5е2 (т.к. е1 и е2 - орты, то е1=е2)
Точно так же строишь сторону ВС, она так же является маленькой гипотенузой с катетами е1 и 5е2, и равна она (26)^1/2*е (т.е. квадратный корень из 26 умноженной на е).
Теперь стороны АВ и ВС надо совместить (см. рисунок в приложении)
Получился треугольник АВС.
Проводим высоту СН, у нас появился прямоугольный треугольник СНВ, чтобы найти СН, при известной стороне ВС нужно знать угол АВС (тогда через синус посчитается), но
угол АВС это сумма углов Альфа и Бетта.
А угол Альфа - это угол прямоуг треугольника с катетами 3е и -4е;
т.е. синус альфа=3е/АВ=3/5, т.е. (по таблице Брадиса) это 37 градусов,
А угол Бетта - это угол прямоугольного треугольника с катетами е1 и 5е2, и гипотенузой ВС.
Тут легче посчитать через тангенс; тангенс Бетта=е1/5е2=1/5, т.е. Бетта=11 градусов (по таблице Брадиса)
Таким образом угол АВС=11+37=48 градусов.
Теперь рассматриваем прямоуг треуг СНВ, где ВС - гипотенуза, СН - катет, и есть угол АВС=48 град,
т.е. синус АВС=СН/ВС
СН=ВС*синусАВС
Подставляй числа, и готово