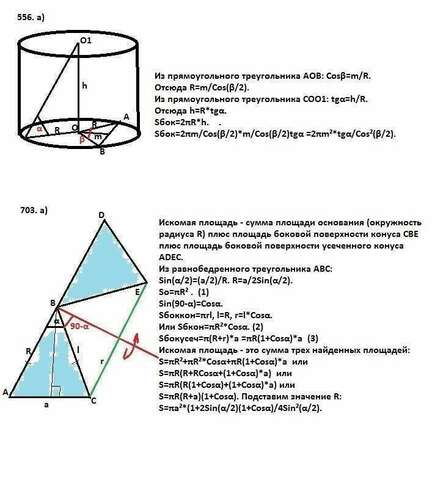
556.а)
Из прямоугольного треугольника АОВ: Cosβ=m/R.
Отсюда R=m/Cos(β/2).
Из прямоугольного треугольника СОО1: tgα=h/R.
Отсюда h=R*tgα.
Sбок=2πR*h. .
Sбок=2πm/Cos(β/2)*m/Cos(β/2)tgα =2πm²*tgα/Cos²(β/2).
703.а)
Искомая площадь - сумма площади основания (окружность радиуса R) плюс площадь боковой поверхности конуса СВЕ плюс площадь боковой поверхности усеченного конуса АDEC.
Из равнобедренного треугольника АВС:
Sin(α/2)=(a/2)/R. R=a/2Sin(α/2).
So=πR²=a²/4Sin²(α/2). (1)
Sin(90-α)=Cosα.
Sбоккон=πrl, l=R, r=l*Cosα.
Или Sбкон=πR²*Cosα. (2)
Sбокусеч=π(R+r)*a =πR(1+Cosα)*a (3)
Искомая площадь - это сумма трех найденных площадей:
S=πR²+πR²*Cosα+πR(1+Cosα)*a или
S=πR(R+RCosα+(1+Cosα)*a) или
S=πR(R(1+Cosα)+(1+Cosα)*a) или
S=πR(R+а)(1+Cosα). Подставим значение R:
S=πa²*(1+2Sin(α/2)(1+Cosα)/4Sin²(α/2).