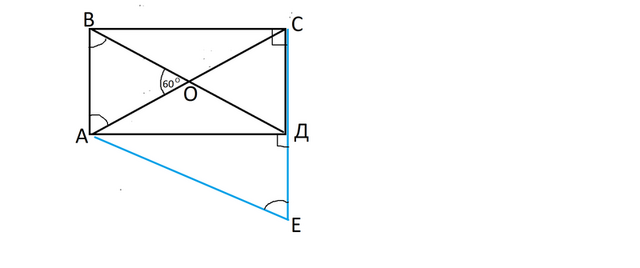
2) Дан прямоугольник АВСД. О- точка пересечения его диагоналей. Известно, что точки А,В,О лежат в плоскости α.
а) Доказать, что точки С и Д также лежат в плоскости α.
Аксиома:
Если плоскости принадлежат две точки прямой, то и вся прямая принадлежит этой плоскости.
Следствие из этой аксиомы:
Одну и только одну плоскость можно провести через две пересекающиеся прямые. Диагонали прямоугольника как раз и есть две пересекающиеся прямые, и все точки этих прямых лежат в одной плоскости.
б) Вычислите S□ АВСД, если АС=8 см, АОВ=60° ( минимум 3 способа)
Треугольник АОВ - равнобедренный ( диагонали прямоугольника равны и точкой пересечения делятся пополам), а так как угол АОВ =60°, то он и равносторонний.
Следовательно, стороны треугольника АОВ равны 8:2=4 см
1) Пристроим к стороне АД треугольник АДЕ, равный треугольнику АСД. Получившийся треугольник АСЕ - равносторонний со сторонами, равными 8 см. Площадь треугольника АСЕ равна площади прямоугольника АВСД
Площадь равностороннего треугольника находят по формуле
SΔ АСЕ=(a²√3):4
SΔ АСЕ =S□ АВСД=(64√3):4=16√3
2) Площадь прямоугольника равна произведению его сторон.
S□ АВСД=АВ*ВС
ВС=АС*sin 60°=(8*√3):2=4√3
S□ АВСД=4*4 √3=16√3
3) Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними. Прямоугольник - параллелограмм:
S□ АВСД= 0,5(8*8*√3):2=16√3
------------------------
Рисунок к задаче 3 дан с ошибкой.
Не указано местонахождение точки Е. Поэтому построить линию пересечения плоскостей РКТ и МСЕ по нему не удастся.