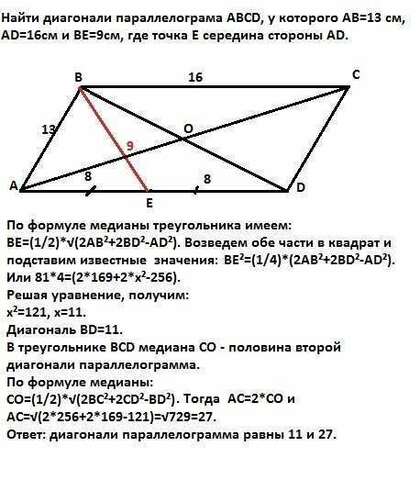
Рассмотрим треугольник АВD.
По формуле медианы треугольника имеем:
ВЕ=(1/2)*√(2АВ²+2ВD²-АD²). Возведем обе части в квадрат и подставим известные значения:ВЕ²=(1/4)*(2АВ²+2ВD²-АD²). Или 81*4=(2*169+2*х²-256). Решая уравнение, получим:
х²=121, х=11.
Диагональ BD=11.
В треугольнике ВСD медиана СО - половина второй диагонали параллелограмма.
По формуле медианы:
СО=(1/2)*√(2ВС²+2СD²-ВD²). Тогда АС=2*СО и
АС=√(2*256+2*169-121)=√729=27.
Ответ: диагонали параллелограмма равны 11 и 27.
P.S. Задачу можно решить и через площади треугольников, помня, что медиана
делит площадь треугольника на два РАВНОВЕЛИКИХ.
По формуле Герона S=√[p(p-a)(p-b)(p-c)], где р- полупериметр, а,b,c - стороны
треугольника. Тогда Sabe=√(15*2*7*6)=√1260.
Sabd=2*Sabe.
Sabd=2*√1260=√[p(p-a)(p-b)(p-c)].
р=(13+16+х)/2 =(29+х)/2.
(р-a)=(x+3)/2.
(p-b)=(x-3)/2.
(p-c)=(29-x)/2.
Тогда Sabd= 2*√1260=√[(29²-х²)(x²-3²)]/4 или, возведя в квадрат,
64*1260=(29²-х²)(x²-3²).
Пусть х²=y. Раскрыв скобки и приведя подобные, получим квадратное
уравнение: y²-850y+88209=0, решив которое, получаем
y1=729 и y2=121, отсюда
х1=27 и х2=11.
То есть, диагонали параллелогпрамма равны 11 и 27.