Найти экстремум функции(решать в виде системы уровнений) z=-1800-x^2-y^2+80x+60y

Question

Дан 1 ответ

GlobeSquare_zn · Answer 1 · 2018-05-11T07:17:10+0000

$z(x,y)=-1800-x^2-y^2+80x+60y$
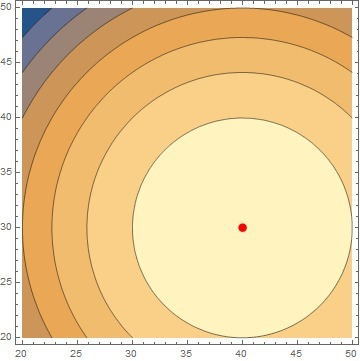
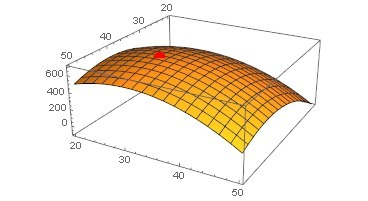
Находим подозрительные на экстремум точки. По необходимому условию экстремума, приравниваем первые частные производные нулю, решаем систему линейных алгебраических уравнений:
$\left \{ {{ \frac{dz}{dx}\equiv80-2x=0, } \atop { \frac{dz}{dy}\equiv60-2y=0, }} \right.=\ \textgreater \ \left \{ {{x=40} \atop {y=30}} \right.$
Из достаточного условия экстремума следует, что если дифф. квадратичная форма положительна, то точка является точкой минимума, если отрицательна - максимума. Составим матрицу H из вторых частных производных заданной функции и вычислим её в стационарной точке (в данном случае элементы H - константы):
$H=\left( \begin{array}{cc} \frac{\partial^2z}{\partial x^2} & \frac{\partial^2z}{\partial x\partial y} \\ \frac{\partial^2z}{\partial x\partial y} &\frac{\partial^2z}{\partial y^2} \\ \end{array} \right)=\left( \begin{array}{cc} -2 & 0 \\ 0 & -2 \\ \end{array} \right)$
Для определения знака квадратичной формы можно воспользоваться критерием Сильвестра: если все угловые миноры матрицы положительны, то квадратичная форма положительна, если у угловых миноров чередуется знак (причём первый отрицательный), то квадратичная форма отрицательна.
Первый элемент <0, а определитель матрицы H >0, следовательно стационарная точка x=40, y=30 является локальным максимумом.
$z(40,30)=700$