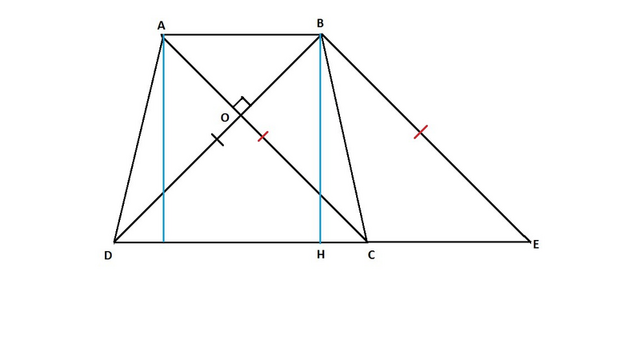
Проведем прямую BE, параллельную стороне АС.
Тогда ABEC - параллелограмм, т.к. BE || AC и BE = AC.
Раз ABEC - параллелограмм, то AB = CE.
Т.к. трапеция равнобедренная, то AC = BD.
BE = AC и BD = AC. Тогда BD = BE => ∆BDE - равнобедренный. Тогда BH - биссектриса, высота и медиана.
Но ∠АОВ = ∠EBD = 90° - как накрест лежащие. Тогда ∠DBH = 1/2•90° = 45°.
∠BDH = 90° - 45° = 45° => ∆DBH - равнобедренный. Тогда DH = BH.
Но т.к. BH - медиана, то DH = 1/2DE.
DE = DC + CE = DC + AB.
Тогда DH = 1/2(DC + AB), т.е. высота равна полусумме оснований.
По определению средняя линия равна тоже полусумме оснований => высота трапеции равна средней линии, значит, средняя линия равна 12.
Ответ: 12.