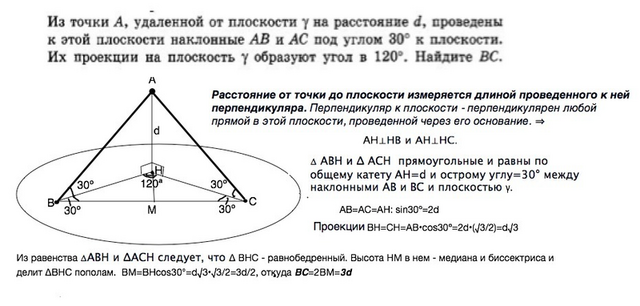
Расстояние от точки до плоскости измеряется длиной проведенного к ней перпендикуляра.Перпендикуляр к плоскости - перпендикулярен любой прямой в этой плоскости, проведенной через его основание. ⇒ АН⊥НВ и АН⊥НС.
∆ АВН и ∆ АСН прямоугольные и равны по общему катету АН=d и острому углу=30° между наклонными АВ и ВС и плоскостью γ.
АВ=АС=АН:sin30º=2d
ПроекцииBH=CH=AB•cos30º=2d•(√3/2)=d√3
Из равенства ∆АВН и ∆АСН следует, что ∆ BHC - равнобедренный. Высота НМ в нем - медиана и биссектриса и делит ∆ВНС пополам.
ВМ=ВН•cos30°=d√3•√3/2=3d/2
BC=2BM=3d