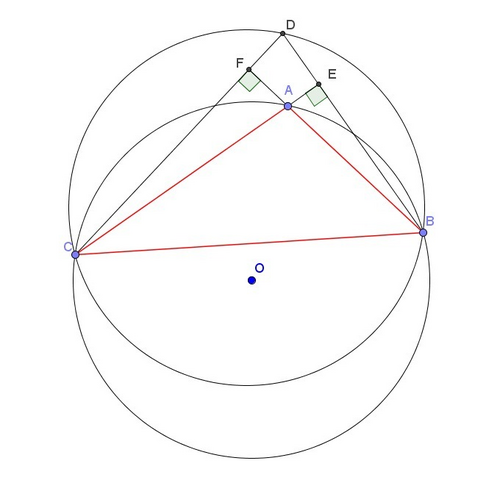
Пусть дан треугольник ABC, у которого ∠A -тупой, CF и BE - его высоты, проведенные к сторонам AB и AC соответственно, и пусть продолжения этих высот пересекаются в точке D. Т.к. угол А - тупой, то D лежит вне ABC.
Тогда ∠CAB=180°-∠CAF. Но ∠CAF=∠CDE, т.к. треугольники CAF и CDE - прямоугольные с общим углом С, т.е. ∠CAB=180°-∠CDE. Значит sin(∠CAB)=sin(180°-∠CDE)=sin(∠CDE)=sin(∠CDB). По теореме синусов радиус окружности, описанной около ABC, равен BC/(2sin(∠CAB)), а радиус окружности, описанной около CDB равен BC/(2sin(∠CDB)). В силу равенства синусов, получаем равенство радиусов этих окружностей, что и требовалось.