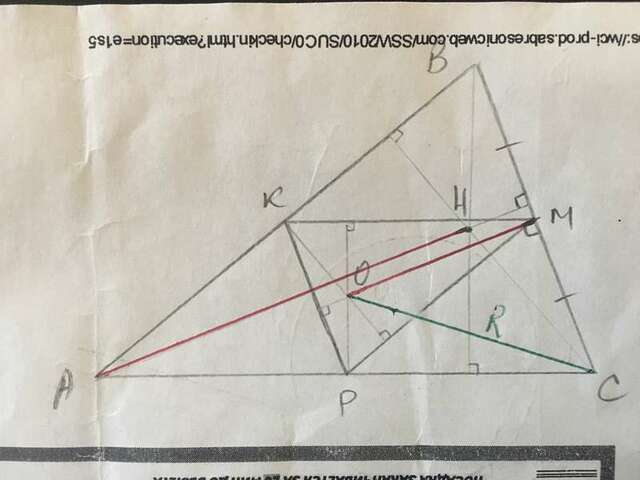
Ортоцентр - это точка пересечения высот треугольника - точка Н.
Центр описанной окружности - это точка пересечения срединных перпендикуляров.
Точки К, М и Р - середины сторон треугольника АВС. Треугольник KМР состоит из средних линий треугольника АВС, значит треугольники подобны с коэффициентом подобия k=2.
Построим срединные перпендикуляры треугольника АВС. Точка О - центр описанной окружности треугольника АВС. Одновременно точка О - ортоцентр треугольника КMP, значит АН=ОМ·k=2ОМ.
МО⊥КР, ВС║КР, значит ОМ⊥ВС.
СМ=ВС/2.
В прямоугольном треугольнике СОМ ОМ=√(ОС²-СМ²)=√(R²-BC²/4).
АН=2√(R²-BC²/4),
AH²=4R²-BC².
Доказано.