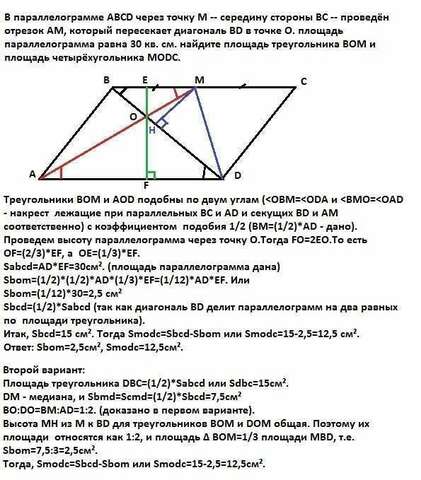
Треугольники ВОМ и АОD подобны по двум углам (Проведем высоту параллелограмма через точку О.Тогда FО=2ЕО.То есть
ОF=(2/3)*EF, a OE=(1/3)*EF.
Sabcd=AD*EF=30см². (площадь параллелограмма дана)
Sbom=(1/2)*(1/2)*AD*(1/3)*EF=(1/12)*AD*EF. Или
Sbom=(1/12)*30=2,5 см²
Sbcd=(1/2)*Sabcd (так как диагональ BD делит параллелограмм на два равных по площади треугольника).
Итак, Sbcd=15 см². Тогда Smodc=Sbcd-Sbom или Smodc=15-2,5=12,5см².
Ответ: Sbom=2,5см², Smodc=12,5см².
Второй вариант:
Площадь треугольника DBC=(1/2)*Sabcd или Sdbc=15см².
DМ - медиана, и Sbmd=Scmd=(1/2)*Sbcd=7,5cм²
ВО:DО=ВМ:АD=1:2. (доказано в первом варианте).
Высота МН из М к ВD для треугольников ВОМ и DОМ общая. Поэтому их площади относятся как 1:2, и площадь ∆ ВОМ=1/3 площади МВD, т.е. Sbom=7,5:3=2,5см².
Тогда, Smodc=Sbcd-Sbom или Smodc=15-2,5=12,5см².