Если не удается подобрать корень перебором, то неплохой вариант - использовать графическое представление.
(х^3)/3 + х^2 - 3х + 2 = 0
(х^3)/3 = -х^2 + 3х - 2
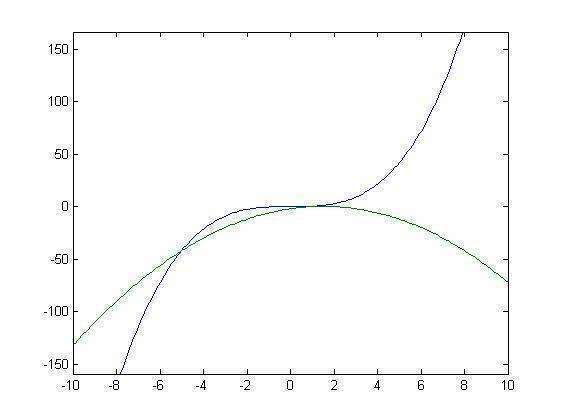
Т.е. имеем кубическую параболу и обычную квадратичную с ветвями вниз.
Прикрепил график. Около нуля пересечения нет, пересечение происходит около -5. Дальше обе функции монотонно уходят в бесконечность, все больше удаляясь друг от друга, так что других пересечений не будет.
Итого, данное уравнение имеет единственный действительный корень.