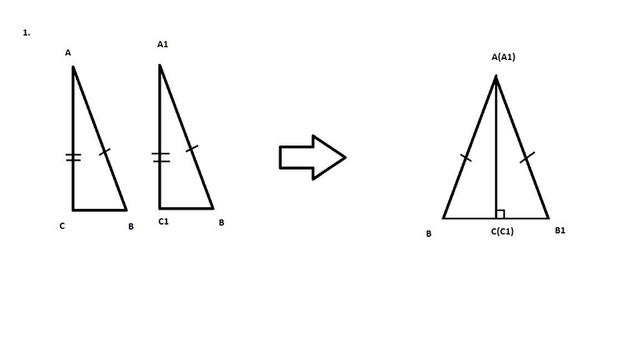
Пусть ABC и A1B1C1 - прямоугольные треугольники, у которых ∠C=∠C1=90°, гипотенуза AB=A1B1 и катет AC=A1C1.
Приложим треугольники друг к другу равными катетами. В итоги получаем равнобедренный треугольник ABB1 с высотой AC, проведенной к основанию. По свойству равнобедренного Δ эта высота еще и медиана, а значит BC=B1C и треугольники ABC и A1B1C1 равны по трем сторонам.
Теорема доказана.