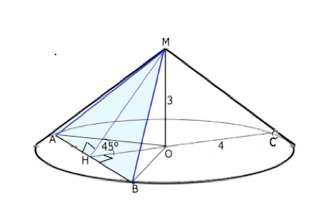
Обозначим хорду АВ, высоту конуса МО, ОА, ОВ и ОС - радиусы основания.
Проведем из О перпендикуляр ОН к хорде. Соединим М с А, В и Н. ∆МАВ - равнобедренный АМ=МВ- образующие.
∠ МНО=45°⇒ ∠НМО=45°, ∆ МОН равнобедренный, и НО=МО=3.
ОН⊥АВ и делит хорду пополам.
Из ∆ ВОН по т.Пифагора катет ВН=√(ОВ²-ОН²)=√(16-9)=√7
По т. о 3-х перпендикулярах МН⊥АВ.
МН - высота ∆МАВ.
МА=МО:sin 45°=3√2
S ∆ МАВ=МН•АВ/2=√7•3√2=3√14
--------------