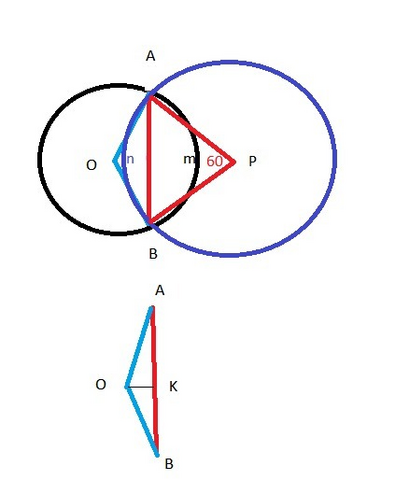
Пусть
РА=РВ=R
ОА=ОВ=r
дуга n 60°; дуга m 120 °
∠APB=60°( центральный угол измеряется дугой n)
ΔAPB- равносторонний ( равнобедренный с углом 60 градусов при вершине)
Значит
АВ=R
∠АОВ=60°
Треугольник АОВ- равнобедренный, АК - высота, медиана и биссектриса
АК=R/2
∠ОАК=30°
r=ОА=АК/cos30°=R/2·(√3/2)=R/√3
S:s=πR²:πr²=(R/r)²=(R/(R/√3))²=3