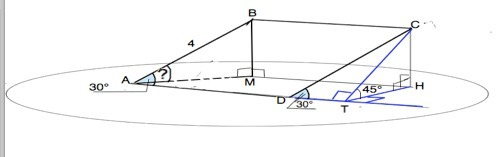
Искомый угол - угол ВАМ в ∆ ВАМ, где ВМ и АМ- катеты, АВ - гипотенуза.
Проведем высоту параллелограмма - перпендикуляр СТ к продолжению АD.
CD=AB=4, угол СDТ=углу ВАD=30°
СТ=СD• sin30° =4•1/2=2
СН ⊥плоскости β, НТ⊥DТ.
∠СТН=45° по условию, откуда СН=2•sin45°=√2
ВС параллельна плоскости β, все ее точки одинаково удалены от неё.
ВМ=СН=√2
sin BAM=BM:AB=(√2):4=0,35355
Ответ: arcos 0,35355 . Это угол 20°42'