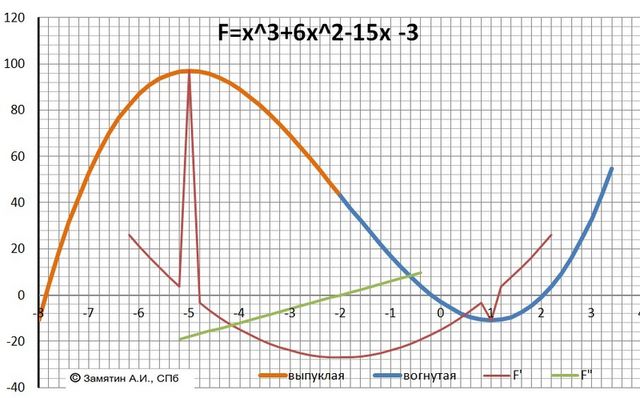
ДАНО
Y= x³ + 6x² -15x - 3 - функция.
НАЙТИ
Локальные экстремумы - критические точки.
РЕШЕНИЕ
Находим первую производную функции.
Y' = 3x² + 12x - 15.
Критические точки - в корнях первой производной -Y'(x)= 0.
Решаем квадратное уравнение.
D = 324 и √324 = 18 и получаем корни
х1 = -5 и х2 = 1.
Находим экстремумы - критические точки
Ymax(-5) = +97 - максимум
Ymin(1) = -11 - минимум
График прилагается.
Дополнительно: В корне второй производной - точка перегиба.