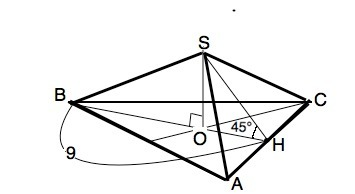
Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания.
Площадь всей поверхности равна сумме площадей основания (S1) и боковой поверхности (S2) пирамиды. .
S=S1+S2
Формула площади правильного треугольника
S=a²√3):4
a=AB=BH:sin60°=9:(√3/2)=6√3
S1=[(6√3)² •√3]:4=27√3
S2=3•SH•AC:2
∆ SOH - равнобедренный прямоугольный.
ОН=1/3 ВН - по свойству точки пересечения медиан треугольника.
ОН=3.
SH=ОН:sin45°=3√2
S2=3•3√2•6√3:2=27√6
S=27√3+27√6=27√3•(1+√2)= ≈112,9 (ед. площади)